1 はじめに

確率に以下のような有名な問題がある (「サンクトペテルブルグの パラドックス」と呼ばれているらしい)。

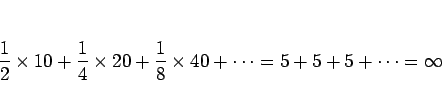
「10 円玉を、表が出るまで投げ続けてくれ。 1 回で表が出れば 10 円あげるが、 2 回目に初めて表が出たら倍の 20 円やろう。 3 回目に初めて表が出たら、さらにその倍の 40 円やる、 という具合に、裏が出続ける度に賞金を倍にする。 これは、期待値は無限大になるから、 100 万円払っても必ずあなたが得をするはずだが、 これを 1 万円払ってやらないかね。」

確かに、この場合の賞金の期待値は、

$$\frac{1}{2}\times 10 + \frac{1}{4}\times 20 + \frac{1}{8}\times 40 + \cdots = 5 + 5 + 5 + \cdots = \infty$$

となるのだが、1 万円でやるかと言われると、 たいていの人が断わるのではないか、という話である。

それは、半分の確率で 10 円、3/4 の確率で 20 円以下にしかならないので、 1 万円だと参加費が高いと感じるからだと思うが、 例えば宝くじもほとんどの人が当たらないのに高額賞金を夢見て 多くの人が実際に宝くじを買っていること、 およびこの賭けの方が期待値ははるかに高いことを考えると、 やや微妙なところである。

それで、これについて、

• 1 万円、および 1000 万円もうかる人はどれくらいの割合でいるのか、 それを宝くじと比較するとどうか
• この賭けを連続して何回続けても構わない場合、 10 円玉を例えば 1000 回投げ続けた場合はいくら位もらえることになるか

などの観点で少し考えてみたいと思う。