次へ: 12 平均回数の数値計算結果 上へ: sort1 前へ: 10 方法 A, B の比較 (PDF ファイル: sort1-2.pdf)


11 増加列ブロック数の分布

$1\sim N$ の $N!$ 通りの順列に対して、増加列ブロック数が どのように分布しているのかを調べることにする。


定義 8

$A^N_k$ = $1\sim N$ の順列の中で、増加列ブロック数が $k$ であるものの個数 ($1\leq k\leq N$)


例えば、$N=3$ のときは、$A^3_1=1$ ((1,2,3) の一つ), $A^3_2=4$, $A^3_3=1$ ((3,2,1) の一つ)、 $N=4$ のときは $(A^4_1,A^4_2,A^4_3,A^4_4)=(1,11,11,1)$ である。 容易に次が言える。

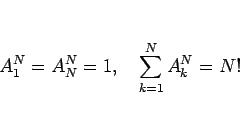
\begin{displaymath} A^N_1=A^N_N=1,\hspace{1zw}\sum_{k=1}^N A^N_k = N! \end{displaymath}

また、対称性
\begin{displaymath} A^N_k = A^N_{N-k+1}\end{displaymath} (3)

も成り立ちそうに見えるが、これはそう難しくなく示される。

例えば、1,3,2,4 は増加列 2 ブロックであるが、これを逆転させた列 4,2,3,1 は増加列 3 (=4-2+1) ブロックになる。 この逆転列の対応を考えると、増加列 2 ブロックのものと 増加列 3 ブロックのものが 1 対 1 に対応することになる。 よって $A^4_2 = A^4_3$ となる。一般の $N$,$k$ の場合も同様である。

以降は、この $A^N_k$ を $N$, $k$ の式で表わすことを考えてみる。 例えば、$N=3$, $k=2$ の場合の $A^3_2$ は、

(1,3,2), (2,1,3), (2,3,1), (3,1,2)
の 4 つであるが、これは 1,2,3 の数字を 2 つの組に分けて、 それぞれを昇順に整列化したものを並べて書いた、と見ることができる:

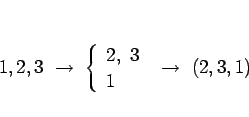
\begin{displaymath} 1,2,3 \rightarrow \left\{\begin{array}{l}2, 3 1\end{array}\right. \rightarrow (2,3,1) \end{displaymath}

1,2,3 を 2 つのブロックに分けるやり方は、 各ブロックに $B_1$, $B_2$ の番号をつけて、 1,2,3 各々がそのどちらに入るかを考えれば $2^3=8$ 通りあるが、 しかしこれには増加列 2 ブロックを生成しない余計なもの 4 つが含まれる:
{(1,2,3),()}, {(1,2),(3)}, {(1),(2,3)}, {(),(1,2,3)} (前の方が $B_1$)
これらは、本来 1 ブロックの並び (1,2,3) に仕切りを入れて分けたものの 個数 $= 3+1 = 4$ に等しい。よって、

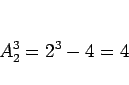
\begin{displaymath} A^3_2 = 2^3-4 = 4 \end{displaymath}

となる。

同様に、$N=4$, $k=2$ の場合は、$2^4$ 通りから (1,2,3,4) に一つの仕切りを 入れる入れ方である 5 通りを引いた

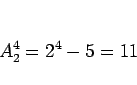
\begin{displaymath} A^4_2 = 2^4 - 5 = 11 \end{displaymath}

となる。

$N=4$, $k=3$ の場合も、1,2,3,4 を 3 つのブロックに分けて それぞれを整列化して並べて書いて、そこから余計なものを引けばよい。 3 つのブロックの分け方の総数は $3^4$、余計なものは、 (1,2),(3),(4) のように、1 ブロックのものを 3 ブロックに分けたもの、 および (1,2),(4),(3) のように、2 ブロックのものを 3 ブロックに分けたもの の 2 種類がある。

2 ブロックのものを 3 ブロックに分けるやり方は、例えば (1,2,4),(3) の場合、

\begin{displaymath} \begin{array}{l} \{(),(1,2,4),(3)\} (\mbox{$B_1$ が空}), ... ... が空}), \{(1,2,4),(3),()\} (\mbox{$B_3$ が空}) \end{array}\end{displaymath}

の 5 通りある ($=$ 5 箇所に 1 つの仕切りを入れる方法)。 2 ブロックは全部で $A^4_2$ だけあるから、 2 ブロックのものを 3 ブロックに分けたものの総数は $5\cdot A^4_2$ となる。

1 ブロックのものを 3 ブロックに分けるやり方は、例えば

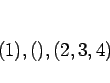
\begin{displaymath} (1),(),(2,3,4) \end{displaymath}

のようになるが、これは 5 箇所に 2 つの仕切りを入れる入れ方で、 ○ 4 つと× 2 つを並べる総数に等しく、よってこれは

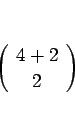
\begin{displaymath} \left(\begin{array}{c} 4+2 2 \end{array}\right) \end{displaymath}

に等しい。よって、結局

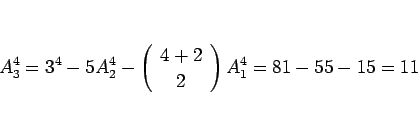
\begin{displaymath} A^4_3 = 3^4 - 5A^4_2 - \left(\begin{array}{c} 4+2 2 \end{array}\right)A^4_1 = 81-55-15 = 11 \end{displaymath}

となる。

これを続けると、結局次の漸化式が得られることになる。

\begin{displaymath} \left\{\begin{array}{lll} A^N_k & = k^N - \displaystyle \s... ...ight)A^N_{k-j} & (k\geq 2),\\ A^N_1 & = 1 \end{array}\right.\end{displaymath} (4)

ここから $A^N_k$ の式を推論するために、2,3 の計算をしてみる。

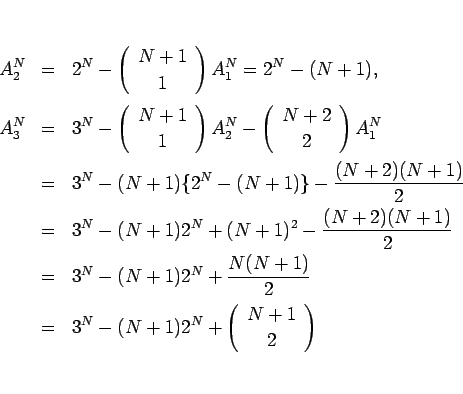
\begin{eqnarray*}A^N_2 &=& 2^N-\left(\begin{array}{c} N+1 1 \end{array}\ri... ...3^N - (N+1)2^N+\left(\begin{array}{c} N+1 2 \end{array}\right)\end{eqnarray*}

同様に、

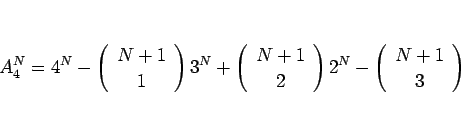
\begin{displaymath} A^N_4 = 4^N-\left(\begin{array}{c} N+1 1 \end{array}\righ... ...}\right)2^N-\left(\begin{array}{c} N+1 3 \end{array}\right) \end{displaymath}

となることも言えるので、一般に、
\begin{displaymath} A^N_k = \sum_{j=0}^{k-1}(-1)^j\left(\begin{array}{c} N+1 j \end{array}\right)(k-j)^N\end{displaymath} (5)

であることが予想される。 これを、(4) を用いて証明する。

そのためにまず、次の補題を示す。


補題 9

全て の $1\leq q\leq N+1$ に対して、次が成り立つ。

\begin{displaymath} \sum_{j=1}^{q}(-1)^{j+1}\left(\begin{array}{c} N+j j \en... ...}\right) = \left(\begin{array}{c} N+1 q \end{array}\right) \end{displaymath} (6)


証明


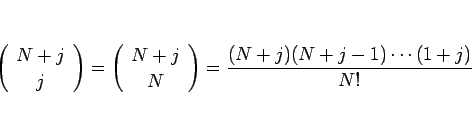
\begin{displaymath} \left(\begin{array}{c} N+j j \end{array}\right) = \left(... ... N \end{array}\right) = \frac{(N+j)(N+j-1)\cdots(1+j)}{N!} \end{displaymath}

であり、これは関数 $x^{N+j}/N!$ を $N$ 回微分した係数、すなわち $N$ 回微分して $x=1$ としたものに等しい:

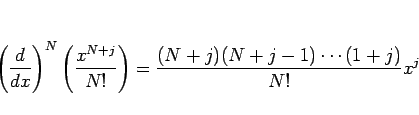
\begin{displaymath} \left(\frac{d}{dx}\right)^N\left(\frac{x^{N+j}}{N!}\right) = \frac{(N+j)(N+j-1)\cdots(1+j)}{N!}x^j \end{displaymath}

よって、
\begin{displaymath} f(x) = \sum_{j=1}^q(-1)^{j+1}\left(\begin{array}{c} N+1 q-j \end{array}\right)\frac{x^{N+j}}{N!} \end{displaymath} (7)

とすれば、(6) の左辺は $f(x)$ を $N$ 回微分して $x=1$ を代入したもの、すなわち $f^{(N)}(1)$ に等しい。

ところで、$f(x)$ は $(N+1)$ から $(N+q)$ 次の項からなる多項式であるが、 これに $x^{N-1}$ 次以下の項をつけ加えても $N$ 回微分には影響はない。 よって、

\begin{displaymath} g(x) = \sum_{j=q-N-1}^q(-1)^{j+1}\left(\begin{array}{c} N+1 q-j \end{array}\right)\frac{x^{N+j}}{N!} \end{displaymath} (8)

とすると、

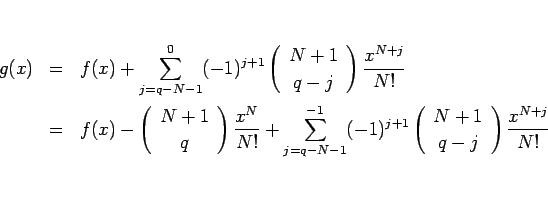
\begin{eqnarray*}g(x) &=& f(x) + \sum_{j=q-N-1}^0(-1)^{j+1}\left(\begin{arra... ...begin{array}{c} N+1 q-j \end{array}\right)\frac{x^{N+j}}{N!} \end{eqnarray*}

となるので、これを $N$ 回微分すると、
\begin{displaymath} g^{(N)}(x) = f^{(N)}(x) - \left(\begin{array}{c} N+1 q \end{array}\right) \end{displaymath} (9)

となる。ところで $g(x)$ は、$j=q-i$ として変形すると

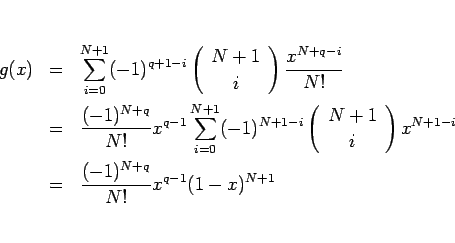
\begin{eqnarray*}g(x) & = & \sum_{i=0}^{N+1}(-1)^{q+1-i}\left(\begin{array}{c... ...ight)x^{N+1-i} &=& \frac{(-1)^{N+q}}{N!}x^{q-1}(1-x)^{N+1} \end{eqnarray*}

であり、$N$ 回微分を行なうと、積の微分で現れる全ての項に 少なくとも $(1-x)^1$ が含まれることになるので、 明らかに $g^{(N)}(1)=0$ である。よって、(9) より

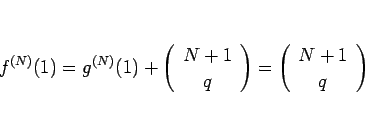
\begin{displaymath} f^{(N)}(1) = g^{(N)}(1) + \left(\begin{array}{c} N+1 q \... ...}\right) = \left(\begin{array}{c} N+1 q \end{array}\right) \end{displaymath}

となって (6) の右辺に等しいことが言える。


(5) の証明

$k$ に関する帰納法により (5) を証明する。

$k=1$ のときは、

\begin{displaymath} % latex2html id marker 2533\mbox{(\ref{eq:ANk:general}) �... ...^0\left(\begin{array}{c} N+1 0 \end{array}\right)(1-0)^N=1 \end{displaymath}

より O.K.

$k=1\sim (m-1)$ に対して (5) が成り立つとして、 $k=m$ に対して (5) が成り立つことを示す ($m\geq 2$)。 (4) より、

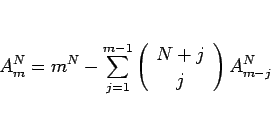
\begin{displaymath} A^N_m = m^N - \sum_{j=1}^{m-1}\left(\begin{array}{c} N+j j \end{array}\right)A^N_{m-j} \end{displaymath}

であるが、右辺の $A^N_{m-j}$ には仮定より (5) が 使えるので、

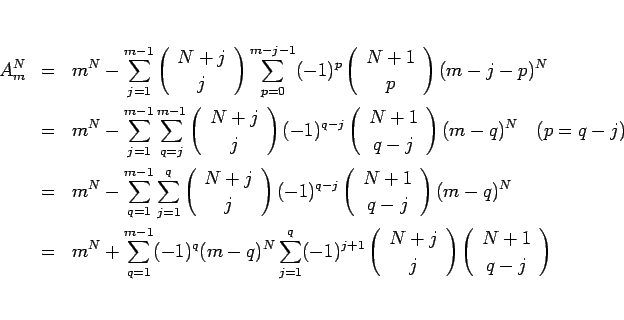
\begin{eqnarray*}A^N_m &=& m^N-\sum_{j=1}^{m-1}\left(\begin{array}{c} N+j \\... ...ray}\right)\left(\begin{array}{c} N+1 q-j \end{array}\right) \end{eqnarray*}

となる。よって、補題 9 により

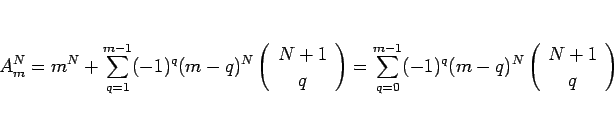
\begin{displaymath} A^N_m = m^N+\sum_{q=1}^{m-1}(-1)^q(m-q)^N\left(\begin{array... ...1)^q(m-q)^N\left(\begin{array}{c} N+1 \ q \end{array}\right) \end{displaymath}

となり、(5) が $k=m$ に対して成り立つことになる。


なお、いくつかの $N$ に対する $A^N_k$ の値を紹介すると、 以下のようにその値は $N$ の増加に対して急激に大きくなることがわかる。

$N$ $(A^N_1,A^N_2,\ldots,A^N_N)$
3 (1, 4, 1)
4 (1, 11, 11, 1)
5 (1, 26, 66, 26, 1)
6 (1, 57, 302, 302, 57, 1)
7 (1, 120, 1191, 2416, 1191, 120, 1)
8 (1, 247, 4293, 15619, 15619, 4293, 247, 1)
9 (1, 502, 14608, 88234, 156190, 88234, 14608, 502, 1)
10 (1, 1013, 47840, 455192, 1310354, 1310354, 455192, 47840, 1013, 1)

次へ: 12 平均回数の数値計算結果 上へ: sort1 前へ: 10 方法 A, B の比較
竹野茂治＠新潟工科大学
2006年2月24日