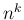
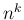 の和の公式に関する考察を紹介した。
通常とは違い、代数的な方法ではなく、
差分方程式の積分による解法を紹介した。
の和の公式に関する考察を紹介した。
通常とは違い、代数的な方法ではなく、
差分方程式の積分による解法を紹介した。
実際には、この和の公式はベルヌーイ数で表現できることが 知られており ([2])、 本稿の手法は、そちらの観点からはあまり意味がないかもしれないが、 初等的な手法しか用いていないので、 高校生でも理解できる内容だと思う。
個人的には、指数 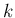 が偶数か奇数かで和の式を求める難易度や、
が偶数か奇数かで和の式を求める難易度や、
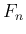 ,
, 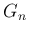 の漸化式の簡便さもだいぶ変わってしまうことが
興味深く感じる。
それは、もしかしたら指数
の漸化式の簡便さもだいぶ変わってしまうことが
興味深く感じる。
それは、もしかしたら指数 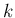 を一般の実数、あるいは複素数に
拡張してその和を
を一般の実数、あるいは複素数に
拡張してその和を 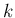 の関数と考えた場合に
その
の関数と考えた場合に
その 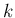 に関する性質として見えてくるかもしれないが、
専門分野ではないのでそのあたりは全くわからない。
に関する性質として見えてくるかもしれないが、
専門分野ではないのでそのあたりは全くわからない。
竹野茂治@新潟工科大学