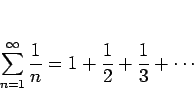次へ: 3 ベキ級数
上へ: 2 無限級数の一般論
前へ: 2.2 絶対収束
(PDF ファイル: series1.pdf)
2.3 収束判定法
無限級数の値を求めることは難しい問題であるが、
それ以前に収束するかどうかを判定することも容易ではなく、
一般的な判定法は残念ながら存在しない。
ここでは、よく用いられる 3 つの判定法を紹介する。
命題 10
正項級数 (1) に対して (
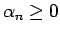 )、
)、
- (ダランベールの判定法)
のとき、
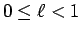 ならば (1) は収束し、
ならば (1) は収束し、
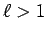 ならば (1) は発散する
ならば (1) は発散する
- (コーシーの判定法)
のとき、
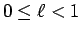 ならば (1) は収束し、
ならば (1) は収束し、
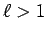 ならば (1) は発散する。
ならば (1) は発散する。
- (積分判定法)
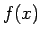 が
が 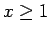 で定義された単調減少関数で、
で定義された単調減少関数で、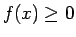 で、
で、
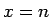 (自然数) に対して
(自然数) に対して 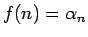 になるとき
(よって
になるとき
(よって 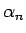 も単調減少数列である必要がある)、
広義積分
も単調減少数列である必要がある)、
広義積分
の収束、発散と (1) の収束、発散は一致する。
証明
1.
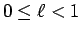 のときは、それが極限であるから、
のときは、それが極限であるから、
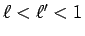 なる
なる 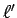 に対して十分大きい
に対して十分大きい 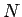 から先の
から先の 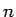 (
(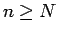 ) に対しては
) に対しては
が成り立つはずである。
よって、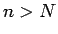 に対して
に対して
となるので、
とすると、
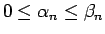 で、
で、
となるので
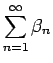 は収束する。
よって
は収束する。
よって
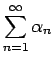 も収束する。
も収束する。
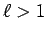 のときは、
のときは、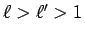 なる
なる 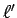 に対して
十分大きい
に対して
十分大きい 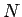 から先の
から先の 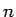 で
で
が成り立つはずなので、
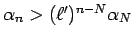 となり、
となり、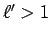 より
より
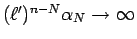 (
(
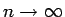 のとき) となるので、
のとき) となるので、
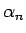 も無限大に発散するので明らかにこの級数は収束しない。
も無限大に発散するので明らかにこの級数は収束しない。
2.
この場合も、1. の場合とほぼ同様。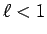 なら、
なら、
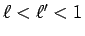 に対してある
に対してある 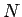 から先の
から先の 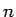 で
で
![$\sqrt[n]{\alpha_n}<\ell'$](img112.gif) が成り立ち、
よって
が成り立ち、
よって
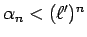 となるので、
となるので、
とすればよい。発散の方も 1. と同様。
3.
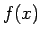 は単調減少関数であるから、
は単調減少関数であるから、
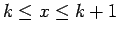 では、
では、
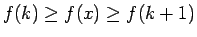 なので、これを
この範囲で積分すると
なので、これを
この範囲で積分すると
が成り立つ (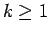 )。よって、
)。よって、
となる。よって、
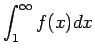 が
が 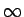 に発散すれば
に発散すれば
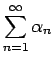 も発散し、
も発散し、
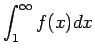 が収束すれば
が収束すれば
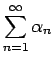 も収束する。
も収束する。
これらの判定法は正項とは限らない級数の場合も適用でき、
例えばダランベールの判定法ならば、一般の級数に対しては、
のとき、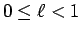 ならば (1) は絶対収束、
ならば (1) は絶対収束、
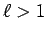 ならば発散、のようになる。
ならば発散、のようになる。
例をいくつか紹介する。
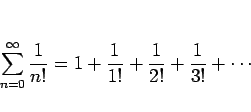 |
(6) |
この級数の場合、ダランベールの判定法により
であるから収束することが言える (実際には 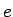 に収束)。
に収束)。
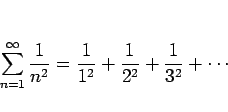 |
(7) |
この場合、
であるから、ダランベールの判定法では収束の判定ができない。
この場合は、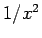 が単調減少関数であり、広義積分は
が単調減少関数であり、広義積分は
となって収束するので、(7) も収束する
(実際には 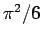 に収束することが知られている)。
一方、
に収束することが知られている)。
一方、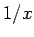 の場合は、
の場合は、
となるので、前にも見たように
は発散する。
次へ: 3 ベキ級数
上へ: 2 無限級数の一般論
前へ: 2.2 絶対収束
竹野茂治@新潟工科大学
2006年9月26日
![]() )、
)、
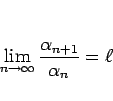
![\begin{displaymath}
\lim_{n\rightarrow\infty}\sqrt[n]{\alpha_n}=\ell
\end{displaymath}](img91.gif)
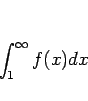
![]() のときは、それが極限であるから、
のときは、それが極限であるから、
![]() なる
なる ![]() に対して十分大きい
に対して十分大きい ![]() から先の
から先の ![]() (
(![]() ) に対しては
) に対しては
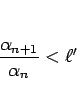
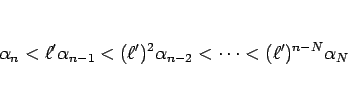
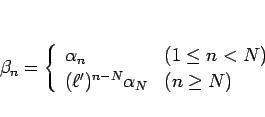
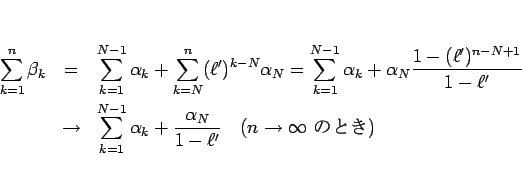
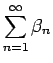 は収束する。
よって
は収束する。
よって
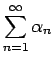 も収束する。
も収束する。
![]() のときは、
のときは、![]() なる
なる ![]() に対して
十分大きい
に対して
十分大きい ![]() から先の
から先の ![]() で
で
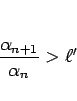
![]() なら、
なら、
![]() に対してある
に対してある ![]() から先の
から先の ![]() で
で
![]() が成り立ち、
よって
が成り立ち、
よって
![]() となるので、
となるので、
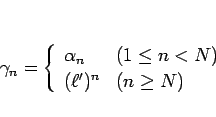
![]() は単調減少関数であるから、
は単調減少関数であるから、
![]() では、
では、
![]() なので、これを
この範囲で積分すると
なので、これを
この範囲で積分すると
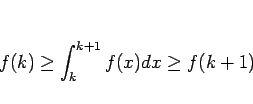
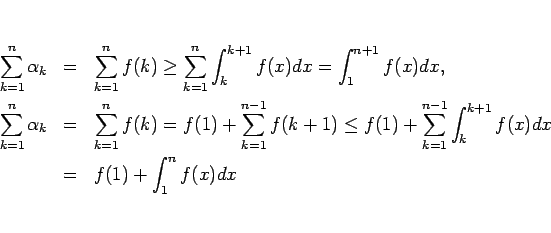
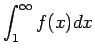 が
が 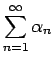 も発散し、
も発散し、
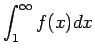 が収束すれば
が収束すれば
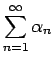 も収束する。
も収束する。
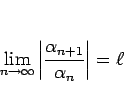
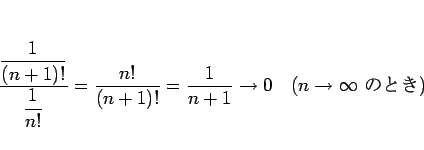
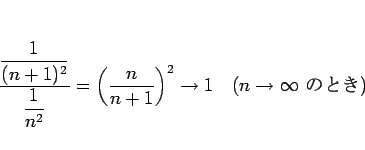
![\begin{displaymath}
\int_1^\infty\frac{dx}{x^2} = \left[-\frac{1}{x}\right]_{x=1...
...w\infty}\left(-\frac{1}{x}\right)-\left(-\frac{1}{1}\right)
=1
\end{displaymath}](img128.gif)
![\begin{displaymath}
\int_1^\infty\frac{dx}{x} = \left[\log\vert x\vert\right]_{x...
...nfty}
=\lim_{x\rightarrow\infty}\log\vert x\vert-\log 1=\infty
\end{displaymath}](img131.gif)