2 設定
メジアンは [1] にあるように中央値を指す。
本稿では度数分布化されているデータを考察することとし、
そのヒストグラムを考える (図 1)。
階級幅を 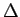 、各階級の代表値を
、各階級の代表値を 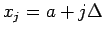 (
(
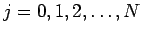 ) とし、各階級の度数を
) とし、各階級の度数を 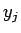 とする。
とする。
階級幅 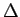 が
が 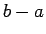 (
(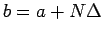 ) に比べてかなり小さいときは、
ヒストグラムは近似的に連続的なグラフ
) に比べてかなり小さいときは、
ヒストグラムは近似的に連続的なグラフ 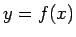 と見ることもできる (図 2)。
と見ることもできる (図 2)。
ただし、総量が決まっている現実のデータでは、
単に階級幅 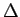 を小さくするだけでは
このような連続的なヒストグラムにはならず、
むしろ階級幅を狭めることで各階級の度数が小さくなり
ヒストグラムの高さが下がっていって、
逆に傾向のわかりにくいものになってしまうことに注意しなければならない (図 3)。
を小さくするだけでは
このような連続的なヒストグラムにはならず、
むしろ階級幅を狭めることで各階級の度数が小さくなり
ヒストグラムの高さが下がっていって、
逆に傾向のわかりにくいものになってしまうことに注意しなければならない (図 3)。
竹野茂治@新潟工科大学
2011年3月18日
![\includegraphics[width=0.5\textwidth ]{hist1.eps}](img2.gif)
![]() が
が ![]() (
(![]() ) に比べてかなり小さいときは、
ヒストグラムは近似的に連続的なグラフ
) に比べてかなり小さいときは、
ヒストグラムは近似的に連続的なグラフ ![]() と見ることもできる (図 2)。
と見ることもできる (図 2)。