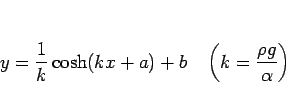 |
(1) |
(1)
この ![]() は定数であるが、
実際にはひもを張った張り具合によって変わるので、
事前に知ることは無理で、これも位置とひもの長さ、
および
は定数であるが、
実際にはひもを張った張り具合によって変わるので、
事前に知ることは無理で、これも位置とひもの長さ、
および ![]() によって決まる値となる。
によって決まる値となる。
さて、この (1) のパラメータ ![]() ,
, ![]() ,
, ![]() を
以下の条件の下で決めるのが今回の話である。
を
以下の条件の下で決めるのが今回の話である。
例えば、山中の送電線などを考えれば、
支える 2 点は必ずしも水平位置にあるとは限らないので、
今回は ![]() とは仮定せずに計算する。
また、実際の電線では、電線の「のび」も考慮する必要があるだろうが、
今回は「のび」は無視して考える。
とは仮定せずに計算する。
また、実際の電線では、電線の「のび」も考慮する必要があるだろうが、
今回は「のび」は無視して考える。
竹野茂治@新潟工科大学