5 空洞世界の力の概算
最後に、前節に考察した、
地中に空洞がある場合のその中でのいくつかの力の大きさを概算してみる。
まず、地底世界の最大の力である地球の自転の遠心力と、
地表での重力との比較を行う。
角速度 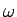 、半径
、半径 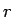 で円運動する質量
で円運動する質量 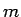 の物体に働く遠心力は
の物体に働く遠心力は
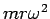 なので、
なので、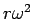 と重力加速度
と重力加速度
![$g=9.8 [\mathrm{m}/\mathrm{s}^2]$](img90.gif) を比較すればよい。
地球の半径
を比較すればよい。
地球の半径 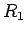 、角速度
、角速度 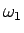 は、
地球の円周がほぼ 40000 [km] =
は、
地球の円周がほぼ 40000 [km] =
![$4.0\times 10^7 [\mathrm{m}]$](img93.gif) なので、
なので、
![\begin{displaymath}
R_1 = \frac{4.0\times 10^7}{2\pi}
= \frac{2.0}{\pi}\times 1...
...60\times 60}
= \frac{\pi}{4.32}\times 10^{-4}[\mathrm{rad/s}]
\end{displaymath}](img94.gif)
より、
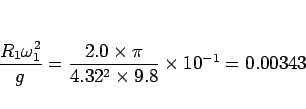 |
(9) |
なので、地表の最大自転遠心力 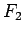 は
地表重力
は
地表重力 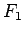 の千分の 3 程度ということになる。
の千分の 3 程度ということになる。
地中の空洞内での最大遠心力はもちろん 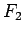 以下であり、
次はそれを打ち消すような小太陽の質量
以下であり、
次はそれを打ち消すような小太陽の質量 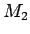 を考えてみる。
空洞内の質量
を考えてみる。
空洞内の質量 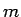 に働く引力の大きさは、
に働く引力の大きさは、
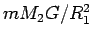 以上であるから、
それが最大遠心力
以上であるから、
それが最大遠心力
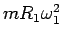 を越えると
どの場所でも中心向きの力が勝ってしまうことになる。
よって、その限界の質量
を越えると
どの場所でも中心向きの力が勝ってしまうことになる。
よって、その限界の質量 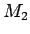 では、
では、
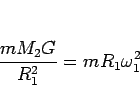
となる。
一方、地球の重力加速度 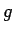 は
ほぼ地球の万有引力によるものに等しいので、
地球の質量
は
ほぼ地球の万有引力によるものに等しいので、
地球の質量 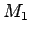
![$(=5.97\times 10^{27}[\mathrm{kg}])$](img104.gif) と (9) により、
と (9) により、
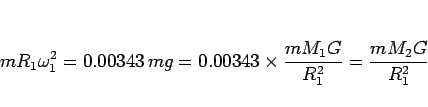
から、結局
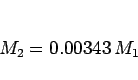 |
(10) |
となる。これよりも大きければ地底世界は全部小太陽に落ちていくことになる。
もしこの小太陽の密度が
太陽の密度
![$\rho_3=1.41\times 10^3 [\mathrm{kg}/\mathrm{m}^3]$](img107.gif) と同じであれば、
その半径を
と同じであれば、
その半径を 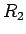 とすると、(10) は
地球の密度
とすると、(10) は
地球の密度
![$\rho_1=5.52\times 10^3 [\mathrm{kg}/\mathrm{m}^3]$](img109.gif) を用いて
を用いて
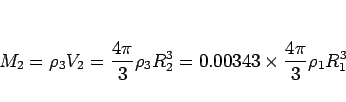
と表され、よって
![\begin{displaymath}
R_2 = R_1\sqrt[3]{0.00343\times\frac{\rho_1}{\rho_3}}
= 0.238 R_1
\end{displaymath}](img111.gif)
となり、地球の半径の約 1/4 程度が限界であることがわかる。
最後に、月や太陽からの引力と地球の重力との比較を行う。
まず太陽質量 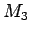 、および太陽と地球の距離
、および太陽と地球の距離 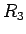 は
は
![\begin{displaymath}
M_3=3.32\times 10^5 M_1,
\hspace{1zw}R_3 = 1.50\times 10^{11} [\mathrm{m}]
= 2.36\times 10^4 R_1
\end{displaymath}](img114.gif)
であり、よって太陽引力の大きさ 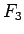 と地表面での重力の大きさ
と地表面での重力の大きさ 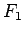 との比は、
との比は、
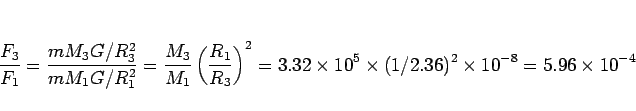
となり、地表重力の 1 万分の 6 程度となる。
月の質量 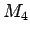 、月と地球の距離
、月と地球の距離 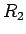 は
は
![\begin{displaymath}
M_4 = 0.0123 M_1,
\hspace{1zw}R_2 = 3.84\times 10^8 [\mathrm{m}]
= 6.03\times 10^1 R_1
\end{displaymath}](img118.gif)
なので、月からの引力 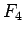 は、
は、
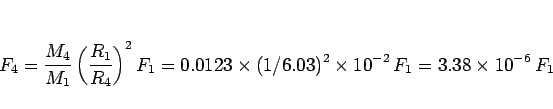
となり、地表重力の 100 万分の 3 程度、ということになる。
地表重力に代わり、最大遠心力 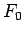 と比較すれば、
と比較すれば、
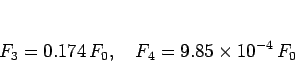
となる。つまり
太陽引力 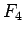 は最大遠心力の 17% なので空洞世界ではかなり影響は強い。
月の引力は最大遠心力の 1000 分の 1 程度なので太陽の引力ほどの影響はないが、
しかしそれでも地表重力に対する太陽の引力の影響 (
は最大遠心力の 17% なので空洞世界ではかなり影響は強い。
月の引力は最大遠心力の 1000 分の 1 程度なので太陽の引力ほどの影響はないが、
しかしそれでも地表重力に対する太陽の引力の影響 (
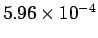 ) よりも桁が一つ大きいので、
それなりの影響があることがわかる。
) よりも桁が一つ大きいので、
それなりの影響があることがわかる。
つまり、地底世界は、外の太陽も月も見えないが、
それら配置の影響をかなり強く受けてしまうことになる。
竹野茂治@新潟工科大学
2013年1月6日
![]() 、半径
、半径 ![]() で円運動する質量
で円運動する質量 ![]() の物体に働く遠心力は
の物体に働く遠心力は
![]() なので、
なので、![]() と重力加速度
と重力加速度
![]() を比較すればよい。
地球の半径
を比較すればよい。
地球の半径 ![]() 、角速度
、角速度 ![]() は、
地球の円周がほぼ 40000 [km] =
は、
地球の円周がほぼ 40000 [km] =
![]() なので、
なので、
![]() 以下であり、
次はそれを打ち消すような小太陽の質量
以下であり、
次はそれを打ち消すような小太陽の質量 ![]() を考えてみる。
空洞内の質量
を考えてみる。
空洞内の質量 ![]() に働く引力の大きさは、
に働く引力の大きさは、
![]() 以上であるから、
それが最大遠心力
以上であるから、
それが最大遠心力
![]() を越えると
どの場所でも中心向きの力が勝ってしまうことになる。
よって、その限界の質量
を越えると
どの場所でも中心向きの力が勝ってしまうことになる。
よって、その限界の質量 ![]() では、
では、
![]() 、および太陽と地球の距離
、および太陽と地球の距離 ![]() は
は