![\includegraphics[height=0.3\textheight]{crv2-earth.eps}](img9.png)
|
地球全体にロープを 1 周させるとその長さは 4万 km ほどになる。 さらにそのロープ全体を地表から 1m の高さに持ち上げた形にするには、 ロープをどれくらい追加しないといけないか。
地球スケールだと一見何 km もつぎ足しが必要なように感じられるが、
答えは地球の半径には無関係で、実はつぎ足しは  m = 6.3m ほどでよい。
これはそういう意外性を目的とした問題である。
m = 6.3m ほどでよい。
これはそういう意外性を目的とした問題である。
なぜそうなるかという説明は通常、半径 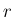 の円周
の円周 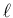 が
が 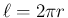 で
あることを利用して、以下のように行われているように思う。
で
あることを利用して、以下のように行われているように思う。
地球の半径をm とすると、最初のロープの長さ
は
m、それを 1m 持ちあげると半径が 1m 増えた円になるので、 その円周
は
m、よってその差は
m となる。
これに対し、以下のような疑問を感じた。
竹野茂治@新潟工科大学