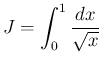 (1)
(1)
普段あまり意識していないかもしれないが、
通常の積分 (正確には「リーマン積分」と言う) は、
「有限区間 ![$[a,b]$](img3.png) 上」の「有界な関数」に対して定義される。
それに対して「広義積分」とはそうではない積分、
すなわち「有限ではない区間での積分」か、
または「有界ではない関数」に対する積分である。
その通常の積分の定義をまず見ておく。
上」の「有界な関数」に対して定義される。
それに対して「広義積分」とはそうではない積分、
すなわち「有限ではない区間での積分」か、
または「有界ではない関数」に対する積分である。
その通常の積分の定義をまず見ておく。
以後、
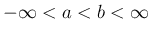 、すなわち、
、すなわち、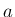 ,
, 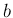 は有限な実数値で
は有限な実数値で 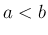 で
あるとし、
で
あるとし、 は閉区間
は閉区間 ![$[a,b]$](img3.png) 上で定義された関数であるする。
上で定義された関数であるする。
![$[a,b]$](img3.png) のひとつの分割を
のひとつの分割を  と書く:
と書く:
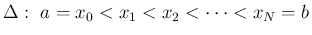
 と書く:
と書く:
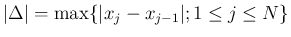
![$[x_{j-1},x_j]$](img13.png) から
ひとつずつ代表点
から
ひとつずつ代表点
![$\xi_j\in[x_{j-1},x_j]$](img14.png) (
(
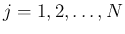 ) を
選び、リーマン和
を作る。リーマン和
) を
選び、リーマン和
を作る。リーマン和 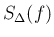 の値は、
分割
の値は、
分割  だけでなく代表点
だけでなく代表点 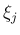 の選び方にも依存する。
の選び方にも依存する。
分割  の分割数
の分割数 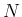 を増やし、
区間の幅
を増やし、
区間の幅 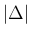 を狭くしていくときに、
リーマン和
を狭くしていくときに、
リーマン和 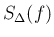 が、
代表点
が、
代表点 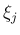 の選び方によらない一定の有限な値
の選び方によらない一定の有限な値 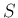 に収束するときに、
に収束するときに、
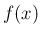 は
は ![$[a,b]$](img3.png) で 積分可能である といい、
その
で 積分可能である といい、
その 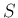 を
を 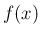 の
の ![$[a,b]$](img3.png) での 定積分 と呼ぶ。
での 定積分 と呼ぶ。
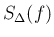 が収束しない、
あるいは代表点
が収束しない、
あるいは代表点 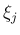 の選び方で
の選び方で 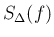 の極限が
変わってしまう場合は、
の極限が
変わってしまう場合は、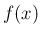 は
は ![$[a,b]$](img3.png) で 積分可能ではない という。
これが、通常の積分 (リーマン積分) の定義である。
で 積分可能ではない という。
これが、通常の積分 (リーマン積分) の定義である。
区間が無限に広い広義積分は、この定義と同列に語れないことは
容易にわかるだろうが、問題は有限区間で有界ではない関数の
広義積分の方である。
この定義では、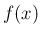 が有界であることには触れていないので、
一見この定義は有界ではない
が有界であることには触れていないので、
一見この定義は有界ではない 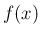 にも
適用できるのではないかと思うかもしれないが、
実はそうではない。
にも
適用できるのではないかと思うかもしれないが、
実はそうではない。
例えば、広義積分としては有限な値になることが知られている (1) の  を例に取って考える。
被積分関数の
を例に取って考える。
被積分関数の 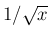 を
を ![$[0,1]$](img24.png) 全体で値を持つように、例えば、
全体で値を持つように、例えば、
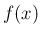 の
の ![$[0,1]$](img24.png) での定積分を考える。
での定積分を考える。
この場合、リーマン和の一番左端を考えると、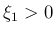 であれば、
であれば、
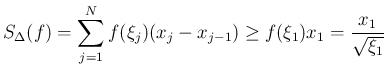
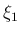 を 0 の近くにとればこの値はいくらでも大きくなる。
つまり、
を 0 の近くにとればこの値はいくらでも大きくなる。
つまり、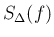 が
「
が
「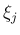 の取り方によらずに有限な値
の取り方によらずに有限な値  に収束すること」はなく、
よって、この関数
に収束すること」はなく、
よって、この関数 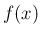 は、通常のリーマン積分の意味では
は、通常のリーマン積分の意味では ![$[0,1]$](img24.png) で積分可能ではないことになる。
で積分可能ではないことになる。
この例からわかるように、有界区間で有界ではない関数は、 通常の積分の定義では積分可能ではない。 よって、そのような関数の積分、すなわち無限に伸びる部分の面積を 意味づけるためには、 通常の積分とは違う形の定義が必要であり、その一つが広義積分なのである。
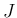 の (2) のような形式的な計算は、
結果的には広義積分と値が一致するものの、普通の積分ではないので、
そのように計算してはいけない、
という意味もなんとなくわかってもらえるのではないかと思う。
の (2) のような形式的な計算は、
結果的には広義積分と値が一致するものの、普通の積分ではないので、
そのように計算してはいけない、
という意味もなんとなくわかってもらえるのではないかと思う。
実は、このような有界ではない関数の積分の意味づけには、 広義積分 (より正確に言えば「広義リーマン積分」) 以外にも、 例えば「ルベーグ積分」と呼ばれるものがある。 リーマン積分の場合は横分割で縦方向に細長い短冊を使って 近似 (リーマン和) するために有界でない関数の近似には向かないのであるが、 それを、むしろ縦に分割する近似を使って 有界でない関数の積分を考えるのがルベーグ積分である。
ルベーグ積分には、有界ではない関数だけでなく、 積分範囲が有限ではない積分も区別なく扱えるというメリットもあるが、 広義リーマン積分とルベーグ積分が常に同じ値になる、 というわけではないし、学ぶのがかなり難しいというデメリットもある。
竹野茂治@新潟工科大学