次へ: 参考文献
上へ: '有理関数の積分について (その 2)'
前へ: 4 積分の計算例
(PDF ファイル: quotef2.pdf)
例を見てもわかると思うが、
[1] で紹介した計算よりもだいぶ易しくなっていることが
わかると思う。
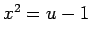 と置くことで
と置くことで 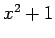 のような式が表に出るのを防いでることと、
全ての次数の項をまとめて未定係数法であつかっているために
それが可能となっているのであるが、
実際には、最終形を頭におかなければ使えないので、
何も見ないでこの方法を使えるかというと、それはそれで問題がある。
のような式が表に出るのを防いでることと、
全ての次数の項をまとめて未定係数法であつかっているために
それが可能となっているのであるが、
実際には、最終形を頭におかなければ使えないので、
何も見ないでこの方法を使えるかというと、それはそれで問題がある。
ただ、部分積分から導かれる漸化式によるのであれば、
それ自体を導く手段をおおまかにたどることで
このような最終形を得るのは容易であるから、
そのような方針で考える、というのも一つの手だと思う。
ただし、最後に見たように、分子が偶数次の項に関しては、
三角関数に置換した後では、
未定係数法を使う方法でも部分積分を使う方法でも
それほどの違いが出るわけではないので、
それについては、未定係数法は選択肢の一つ、という程度かもしれない。
次へ: 参考文献
上へ: '有理関数の積分について (その 2)'
前へ: 4 積分の計算例
竹野茂治@新潟工科大学
2006年6月2日