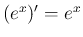
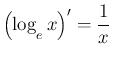 (
(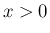 )
)
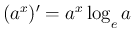
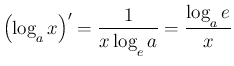 (
(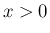 )
)
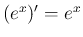
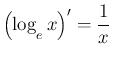 (
(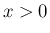 )
)
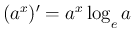
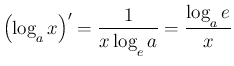 (
(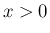 )
)
教科書 [1] では、これらを以下の順で示している。
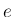 の定義 (教科書 p11 下):
の定義 (教科書 p11 下):
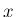 に拡張でき、さらに
に拡張でき、さらに
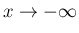 でも
同じものに収束 (教科書 (1.1)):
でも
同じものに収束 (教科書 (1.1)):
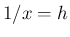 としたもの (教科書 p13 上):
としたもの (教科書 p13 上):
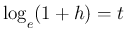 とすると
得られるもの (教科書公式 1.5):
とすると
得られるもの (教科書公式 1.5):
上の 2. の (2) については教科書には詳しい説明はないが、
それは以前 [2] で説明をした。
その他、7., 8. 以外は教科書に書いてある通りなので、以下で 7., 8. の
説明をする。
なお、7., 8. の証明が教科書 [1] に書いてないのは、
多分 7. の方は、その直前に書いてある 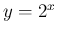 の微分の対数微分法による例で
一般の
の微分の対数微分法による例で
一般の 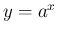 の場合もわかるだろう、ということだと思われるし、
8. の方は、公式としなくても底の変換を行えばすぐに計算できるだろう、
ということだと思われる。
の場合もわかるだろう、ということだと思われるし、
8. の方は、公式としなくても底の変換を行えばすぐに計算できるだろう、
ということだと思われる。
まず、7. は、いわゆる「対数微分法」を使うのであるが、 それは合成関数の微分の応用なので、 ここでは公式 2 と合成関数の微分を組み合わせることで、 公式 3 が成り立つことを示す。
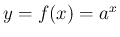 とし、この微分を考える。
とし、この微分を考える。
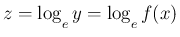
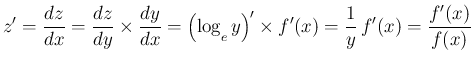
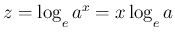 より
より
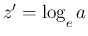 と
なる。よって、
と
なる。よって、
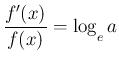
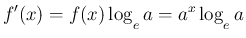
次は 8。これは、底の変換により

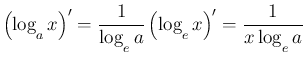
解析学の教科書の多くが、似たような流れで指数関数、対数関数の 導関数の証明を紹介しているが、 公式 3 の証明については対数微分法以外にも、 公式 1 から得る方法もあるし、公式 4 から得る方法もあり、 そういう証明を採用している教科書も少なくない。
竹野茂治@新潟工科大学