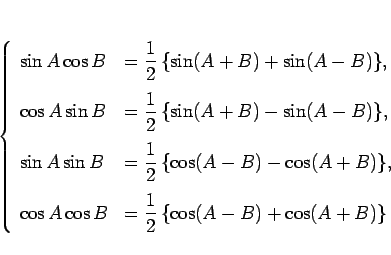 |
(14) |
積→和の公式とは、加法定理から得られる以下の公式である。
(14)
例えば、4 節の ![]() の計算に出てきた 3 乗の項は以下のように変形できる。
の計算に出てきた 3 乗の項は以下のように変形できる。
この方法の難点は、積→和の公式自体が面倒であることと、
それによる変形もそれなりに面倒なことだろう。
さらに、元の関数が累乗の形であるのに対して、
この方法による結果はすべて ![]() のように累乗ではない形なので、
累乗の形で解を求めたい場合には、
その結果を加法定理で展開をしなければいけない点も、
場合によっては欠点となるかもしれない。
のように累乗ではない形なので、
累乗の形で解を求めたい場合には、
その結果を加法定理で展開をしなければいけない点も、
場合によっては欠点となるかもしれない。
竹野茂治@新潟工科大学