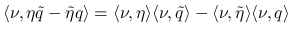 (1)
(1)
元の方程式は, 1 次元の等エントロピー流を記述する保存則形の 偏微分方程式
で,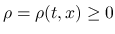 は気体密度,
は気体密度, 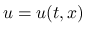 は速度,
は速度,
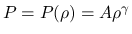 は圧力,
は圧力, 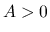 ,
, 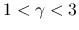 は定数で,
は定数で, 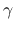 は断熱指数とも呼ばれる.
前者は質量保存則, 後者は運動量保存則を意味し, よって (3) は「連立保存則方程式」とも呼ばれる.
は断熱指数とも呼ばれる.
前者は質量保存則, 後者は運動量保存則を意味し, よって (3) は「連立保存則方程式」とも呼ばれる.
この方程式の初期値問題の解の存在証明方法として, 補償コンパクト性理論 (compensated compactness theory) という
ものがあり, それを用いて, 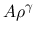 形の圧力に対しては, 大きさや変動に制限をつけない初期値に対する (3) の
初期値問題の弱解の存在が, まず DiPerna (1983)[3] によって
断熱指数
形の圧力に対しては, 大きさや変動に制限をつけない初期値に対する (3) の
初期値問題の弱解の存在が, まず DiPerna (1983)[3] によって
断熱指数 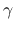 が
が
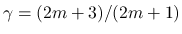 (
(
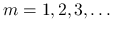 ) の
場合に示され, Ding-Chen-Luo (1985,1986)[2] によってそれが
任意の
) の
場合に示され, Ding-Chen-Luo (1985,1986)[2] によってそれが
任意の
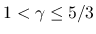 に拡張され, Lions-Perthame-Tadmor (1994)[5] により
に拡張され, Lions-Perthame-Tadmor (1994)[5] により 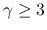 の場合, そして Lions-Perthame-Souganidis (1996)[4] により
の場合, そして Lions-Perthame-Souganidis (1996)[4] により 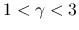 の
場合が示され, 等エントロピー流の
の
場合が示され, 等エントロピー流の
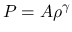 の形に対しては,
の形に対しては, 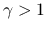 のすべての
のすべての 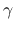 に対して弱解の問題はほぼ解決している.
に対して弱解の問題はほぼ解決している.
その後もその理論を適用できる圧力項 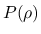 を広げる試みが行われて
いるが (Chen-LeFloch[1], Makino[7], Lu[6]), それには従来の証明の方針自体の見直しも必要になる.
また, DiPerna (1983)[3] の結果に対する拡張である Ding-Chen-Luo[2] の方法は, 長大な計算の連続であるためその読解も難しく, それらの証明の改良, 簡略化も, この分野の発展のためには必要だと思われる.
を広げる試みが行われて
いるが (Chen-LeFloch[1], Makino[7], Lu[6]), それには従来の証明の方針自体の見直しも必要になる.
また, DiPerna (1983)[3] の結果に対する拡張である Ding-Chen-Luo[2] の方法は, 長大な計算の連続であるためその読解も難しく, それらの証明の改良, 簡略化も, この分野の発展のためには必要だと思われる.
本稿では, Ding-Chen-Luo[2] らの証明の改良の前段階として, DiPerna[3] の結果, すなわち
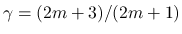 の場合に
対する証明の, 特に Tartar 方程式の解法部分に関する若干の改良を紹介する.
の場合に
対する証明の, 特に Tartar 方程式の解法部分に関する若干の改良を紹介する.
なお, Ding-Chen-Luo[2] は DiPerna[3] の方法を
そのまま実数の 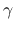 に拡張したものなので, 本稿の手法は Ding-Chen-Luo[2] の方法にも適用が
可能であるが, Lions-Perthame-Tadmor[5], Lions-Perthame-Souganidis[4] の手法は, DiPerna[3] や Ding-Chen-Luo[2] らの Darboux エントロピーではなく, 核エントロピーを用いた方法なので, 本稿の改良はそれらには当てはまらない.
むしろ, 逆に本稿の改良は, Lions らの方法[5,4] から
ヒントを得ている部分もある.
に拡張したものなので, 本稿の手法は Ding-Chen-Luo[2] の方法にも適用が
可能であるが, Lions-Perthame-Tadmor[5], Lions-Perthame-Souganidis[4] の手法は, DiPerna[3] や Ding-Chen-Luo[2] らの Darboux エントロピーではなく, 核エントロピーを用いた方法なので, 本稿の改良はそれらには当てはまらない.
むしろ, 逆に本稿の改良は, Lions らの方法[5,4] から
ヒントを得ている部分もある.
竹野茂治@新潟工科大学