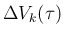
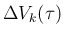 は、
は、
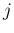 以外の特性族に出る front の世代は
以外の特性族に出る front の世代は 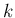 以上で、
(55) より
以上で、
(55) より
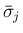 の
世代も
の
世代も 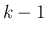 以下となり、よって
以下となり、よって 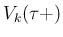 は
は
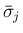 を
含まない。
を
含まない。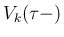 は
は 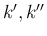 のうち
のうち 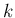 以上のものがあれば
それを含むが、結局
以上のものがあれば
それを含むが、結局
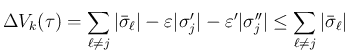
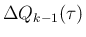 は、
は、
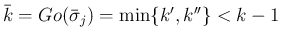 となる。
となる。
3.6 節の 2. を除いた 5 通りで場合分けし、
まず 1. の 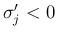 ,
, 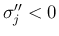 ,
,
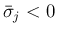 のときを考える。
のときを考える。
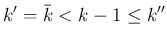
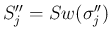 だが
だが
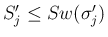 で、
で、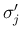 と
と
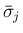 は
世代が同じなので、結局
は
世代が同じなので、結局 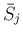 とそれらの大小関係は
となる。よって、この場合、
とそれらの大小関係は
となる。よって、この場合、
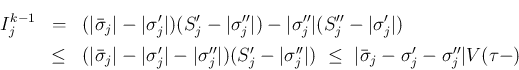
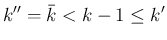
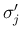 と
と 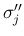 等を入れかえるだけで
同様の評価ができ、結局いずれの場合も
が得られる。
等を入れかえるだけで
同様の評価ができ、結局いずれの場合も
が得られる。
次は 3. の 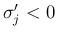 ,
, 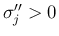 ,
,
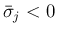 の場合。
の場合。
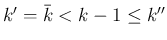 の場合は
の場合は
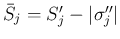 で、
で、
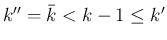 の場合は
の場合は
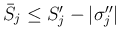 なので、いずれの場合も、
なので、いずれの場合も、
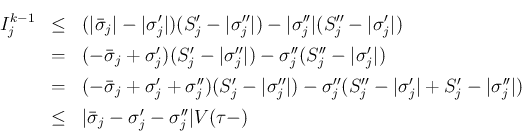
5. の場合は、3. の場合の 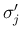 と
と 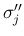 の入れかえなので、
同じく (61) が得られる。
の入れかえなので、
同じく (61) が得られる。
次は 4. の 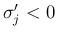 ,
, 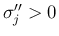 ,
,
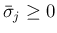 の場合。
の場合。
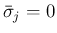 ならば明らかに
ならば明らかに
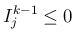 となり (61) が成り立つので、
となり (61) が成り立つので、
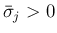 の場合を考える。
の場合を考える。
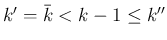 の場合は
の場合は
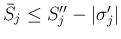 で、
で、
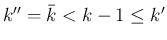 の場合は
の場合は
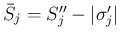 なので、
いずれの場合も、
なので、
いずれの場合も、
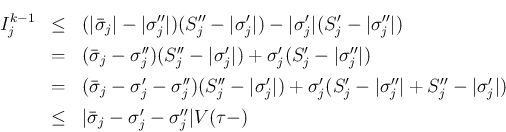
6. も、4. の 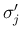 と
と 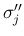 の入れかえなので、
同じく (61) が得られる。
の入れかえなので、
同じく (61) が得られる。
よって、[A-2] の場合はすべて (61) が
成り立ち、、(58), (61) により、
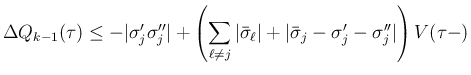
竹野茂治@新潟工科大学