(PDF ¥Õ¥¡¥¤¥ë: bib.pdf)

References

1

G.-Q.Chen. Convergence of the Lax-Friedrichs scheme for isentropic gas dynamics (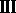). Acta Mathematica Scientia 6(1986), 75-120 (Chinese edition: 8(1988), 101-134).

2

G.-Q.Chen. The compensated compactness method and the system of isentropic gas dynamics. Mathematical Sciences Research Institute, Berkeley, 1990.

3

G.-Q.Chen. The method of quasidecoupling for discontinuous solutions to conservation laws. Arch. Rational Mech. Anal. 121 (1992), 131-185.

4

G.-Q.Chen and J.Glimm. Global solutions to the compressible Euler equations with geometrical structure. Comm. Math. Phys.180(1996), 153-193.

5

G.-Q.Chen and P.T.Kan. Hyperbolic conservation laws with umbilic degeneracy I. Arch. Rational Mech. Anal. 130(1995), 231-276.

6

G.-Q.Chen, C.D.Levermore and T.P.Liu. Hyperbolic conservation laws with stiff relaxation terms and entropy. Comm. Pure Appl. Math.47(1994), 787-830.

7

G.-Q.Chen and T.P.Liu. Zero relaxation and dissipation limits for hyperbolic conservation laws. Comm. Pure Appl. Math. 46(1993), 755-781.

8

G.-Q.Chen, D.Wang. Convergence of shock capturing schemes for the compressible Euler-Poisson equations. Comm. Math. Phys.179(1996), 333-364.

9

K.N.Chueh, C.C.Conley and J.A.Smoller. Positively invariant regions for systems of nonlinear diffusion equations. Indiana Univ. Math. J. 26(1977), 373-392.

10

B.Dacorogna. Weak continuity and weak lower semicontinuity of Non-linear functionals Lecture Note in Math.922, Springer, 1982.

11

X.Ding, G.-Q.Chen, and P.Luo. Convergence of the Lax-Friedrichs scheme for isentropic gas dynamics ()-()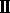. Acta Mathematica Scientia 5(1985), 415-432, 433-472 (Chinese edition: 7(1987), 467-481; 8(1988), 61-94).

12

X.Ding, G.-Q.Chen and P.Luo. A supplement to the papers 'Convergence of the Lax-Friedrichs scheme for isentropic gas dynamics (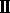)-()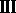'. Acta Mathematica Scientia 9(1989), 43-44.

13

X.Ding, G.-Q.Chen and P.Luo. Convergence of the fractional step Lax-Friedrichs scheme and Godunov scheme for the isentropic system of gas dynamics. Comm. Math. Phys. 121(1989), 63-84.

14

R.J.DiPerna. Convergence of approximate solutions to conservation laws. Arch. Rational Mech. Anal. 82(1983), 27-70.

15

R.J.DiPerna. Convergence of viscosity method for isentropic gas dynamics. Comm. Math. Phys. 91(1983), 1-30.

16

L.C.Evans. Weak convergence methods for nonlinear partial differential equations CBMS regional conference ser. in Math. 74, AMS, 1990.

17

E.Feireisl. Time-periodic solutions to quasilinear telegraph equations with large data. Arch. Rational Mech. Anal. 112(1990), 45-62.

18

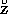
M.Kru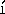k. Explicit characterization of 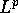-Young measures. J. Math. Anal. Appl. 198(1996), 830-843.

19

P.Lin. Young measures and an application of compensated compactness to one-dimensional nonlinear elastodynamics. Trans. Amer. Math. Soc. 329(1992), 377-413.

20

P.L.Lions, B.Perthame and E.Tadmor. Kinetic formulation of the isentropic gas dynamics and p-systems. Comm. Math. Phys. 163(1994), 415-431.

21

T.Makino and S.Takeno. Initial boundary value problem for the spherically symmetric motion of isentropic gas. Japan J. Indust. Appl. Math. 11(1994), 171-183.

22

P.Marcati and R.Natalini. Weak solutions to a hydrodynamic model for semiconductors and relaxation to the drift-diffusion equation. Arch. Rational Mech. Anal. 129(1995), 129-145.

23

P.Marcati and R.Natalini. Global weak entropy solutions to quasilinear wave equations of Klein-Gordon and Sine-Gordon type. preprint (1996), 1-23.

24

J.M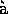lek, J.Ne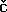as, M.Rokyta and M.R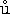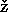i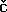ka. Weak and measure-valued solutions to evolutionary PDEs. Chapman & Hall, London, 1996.

25

J.A.Nohel, R.C.Rogers and A.E.Tzavaras. Weak solutions for a nonlinear system in viscoelasticity. Comm. Partial Differential Equations 13(1988), 97-127.

26

B.Rubino. Compactness framework and convergence of Lax-Friedrichs and Godunov schemes for a 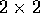nonstrictly hyperbolic system of conservation laws. Quart. Appl. Math. 53(1995), 401-421.

27

W.Rudin. Real and complex analysis. McGraw-Hill, New York 1996.

28

M.E.Schonbek. Convergence of solutions to nonlinear dispersive equations. Comm. Partial Differential Equations 7(1982), 959-1000.

29

D.Serre. La compacit 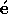par compensation pour les syst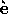mes hyperboliques non lin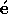aires de deux 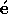quations a une dimension d'espace. J. Math. Pures Appl. 65(1986), 423-468.

30

D.Serre. Syst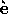mes de lois de conservation , 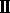Diderot, Paris 1996.

31

J.Shearer. Global existence and compactness in 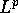for the quasi-linear wave equation. Comm. Partial Differential Equations 19(1994), 1829-1877.

32

J.Smoller. Shock waves and reaction-diffusion equations. (2nd edition), Springer, 1991.

33

S.Takeno. Initial boundary value problem for isentropic gas dynamics. Proc. Royal Soc. Edinburgh 120A(1992), 1-23.

34

S.Takeno. Free piston problem for isentropic gas dynamics. Japan J. Indust. Appl. Math. 12(1995), 163-194.

35

S.Takeno. A time-periodic solution for a scalar conservation law. preprint (1996), 1-26.

36

L.Tartar. Compensated compactness and applications to partial differential equations. 136-211, Nonlinear analysis and mechanics: Heriot-Watt Symposium, Vol.4, ed. R.J.Knops, Research Notes in Mathematics 39, Pitman, London 1979.

37

L.Tartar. The compensated compactness method applied to systems of conservation laws. 263-285, Systems of nonlinear partial differential Equations, ed. J.M.Ball, NATO ASI Series, 1983.

38

B.Zhang. Convergence of the Godunov scheme for a simplified one-dimensional hydrodynamic model for semiconductor devices. Comm. Math. Phys. 157(1993), 1-22.

39

Y.Zhou. An 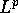theorem for compensated compactness. Proc. Royal Soc. Edinburgh 122A(1992), 177-189.