同様の考え方で、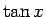 の導関数も考えることができる (図 5)。
の導関数も考えることができる (図 5)。
図 5:
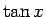 の微分
の微分
|
|
この場合、D の  座標が
座標が 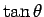 , F の
, F の 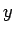 座標が
座標が
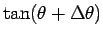 なので、
なので、
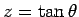 の増分は、
の増分は、
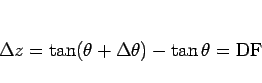
となる。
一方、扇形 OBC と ODE は相似で、OB:OD=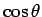 :1 より、
:1 より、
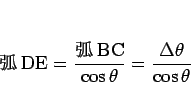
であり、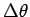 が 0 に近ければ、
が 0 に近ければ、
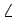 ODE と
ODE と 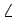 OED は直角に近く、
DEF も
OED は直角に近く、
DEF も 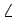 E が直角の直角三角形で近似できる。
この場合、
E が直角の直角三角形で近似できる。
この場合、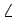 EDF もほぼ
EDF もほぼ 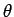 に近いので、よって
に近いので、よって
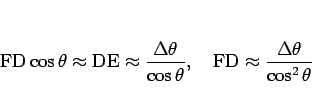
が得られる。ゆえに
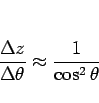
となり、その極限として
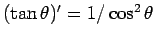 が
得られることになる。
が
得られることになる。
竹野茂治@新潟工科大学
2014年7月2日