| 数学ライブラリ関数 |
| 関数 |
引数 |
戻り値 |
|
abs(x) |
任意 |
x
の絶対値, | x|
; 同じ型 |
| abs(x) |
複素数 |
x
の長さ,
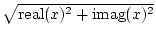
|
|
acos(x) |
任意 |
cos-1x
(アークコサイン) |
|
acosh(x) |
任意 |
ラジアンでの
cosh-1x
(逆双曲余弦) |
|
arg(x) |
複素数 |
x
の偏角 |
|
asin(x) |
任意 |
sin-1x
(アークサイン) |
|
asinh(x) |
任意 |
ラジアンでの
sinh-1x
(逆双曲正弦) |
|
atan(x) |
任意 |
tan-1x
(アークタンジェント) |
|
atan2(y,x) |
整数または実数 |
tan-1(y/x)
(アークタンジェント) |
|
atanh(x) |
任意 |
ラジアンでの
tanh-1x
(逆双曲正接) |
|
besj0(x) |
整数または実数 |
x
の j0
ベッセル関数 |
|
besj1(x) |
整数または実数 |
x
の j1
ベッセル関数 |
|
besy0(x) |
整数または実数 |
x
の y0
ベッセル関数 |
|
besy1(x) |
整数または実数 |
x
の y1
ベッセル関数 |
|
ceil(x) |
任意 |
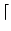 x x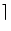 , x
以上の最小の整数(real part)
, x
以上の最小の整数(real part) |
|
cos(x) |
任意 |
x
のコサイン cos x
|
|
cosh(x) |
任意 |
cosh x
, x
のハイパボリックコサイン |
|
erf(x) |
任意 |
erf(real(x))
, x
の 実部の誤差関数 |
|
erfc(x) |
任意 |
erfc(real(x))
, 1.0 - (x
の実部の誤差関数) |
|
exp(x) |
任意 |
ex
, x
の指数関数 |
|
floor(x) |
任意 |
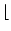 x x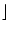 , x
(の実部) 以下の最大の整数
, x
(の実部) 以下の最大の整数 |
|
gamma(x) |
任意 |
gamma(real(x))
, x
の実部のガンマ関数 |
|
ibeta(p,q,x) |
任意 |
ibeta(real(p, q, x))
, p
,q
,x
の実部の不完全ベータ関数 |
|
inverf(x) |
任意 |
x
の実部の逆誤差関数 |
|
igamma(a,x) |
任意 |
igamma(real(a, x))
, a
,x
の実部の不完全ガンマ関数 |
|
imag(x) |
複素数 |
x
の虚数部分 (実数) |
|
invnorm(x) |
任意 |
x
の実部の逆正規分布関数 |
|
int(x) |
実数 |
x
の実数部分 (0 に向かって丸め) |
|
lambertw(x) |
実数 |
Lambert W 関数 |
|
lgamma(x) |
任意 |
lgamma(real(x))
, x
の実部のガンマ対数関数 |
|
log(x) |
任意 |
logex
, x
の自然対数 (底 e
) |
|
log10(x) |
任意 |
log10x
, x
の対数 (底 10
) |
|
norm(x) |
任意 |
x
の実部の正規分布 (ガウス分布) 関数 |
|
rand(x) |
任意 |
rand(real(x))
, 疑似乱数生成器 |
|
real(x) |
任意 |
x
の実部 |
|
sgn(x) |
任意 |
x > 0
なら 1, x < 0
なら -1, x = 0
なら 0. x
の虚部は無視 |
|
sin(x) |
任意 |
sin x
, x
のサイン |
|
sinh(x) |
任意 |
sinh x
, x
のハイパボリックサイン |
|
sqrt(x) |
任意 |
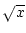 , x
の平方根
, x
の平方根 |
|
tan(x) |
任意 |
tan x
, x
のタンジェント |
|
tanh(x) |
任意 |
tanh x
, x
のハイパボリックタンジェント |